|
Article tiré de la revue
Electronique Pratique Novembre 1994. Auteur : F. JONGBLOET.
Sommaire
:
Filtrage
analogique
Rôle
et caractéristique d'un filtre
Les
différents types de filtres
Pour
bien comprendre le rôle d'un filtre dans un système électronique, il faut
garder présent à l'esprit le fait que ceux-ci agissent sur des signaux
électriques (tensions et/ou courants) dont ils vont modifier certaines
caractéristiques.
I -
filtrage analogique
Nous
raisonnerons dans la suite de cet exposé sur des tensions, mais toutes les
notions abordées pourront être étendues aux courants sans aucun problème. Etant
donné qu'un filtre agit sur le spectre des signaux qui lui sont appliqués, nous
commencerons par définir cette notion, ce qui nous conduira à distinguer les
signaux périodiques de ceux qui ne le sont pas.
1 ° Spectre d'un signal périodique :
Tout signal périodique v(t) de période T,
fréquence f = 1/T (pulsation w = 6,28 f), possédant un
nombre fini d'extréma et de discontinuités (conditions dites de Diriclet), est
décomposable en une somme de fonctions sinusoïdal qui prend le nom de série de
Fourier, du nom du mathématicien qui s'est occupé de cette analyse.

Figure
1 : Décomposition
d'un signal en série de Fourrier
La décomposition en série de Fourier d'un
signal carré ne comporte pas d'harmoniques de rang pair ni de termes en
cosinus, ce qui peut se justifier très simplement en remarquant que le signal
étudié est impair [
v(t) = - v(-t) ] et que, de plus, [
v(t + T/2) = - v(t) ].
On remarque en outre que la valeur moyenne est nulle et que les amplitudes des
différents termes de la décomposition en série de Fourier (que l'on appelle
aussi des raies du spectre) ont des amplitudes qui décroissent en 1/n, avec n,
le rang de l'harmonique.
La représentation graphique donnant
l'amplitude de chacun des termes de la décomposition en série de Fourier en
fonction de la fréquence (fig.2) s'appelle un spectre d'amplitude. Les
fréquences présentes dans ce spectre sont parfois, appelées composantes
spectrales et plus simplement "raies", par analogie avec le domaine de
l'optique. Le mode de décroissance de l'amplitude des composantes spectrales
d'un signal avec le rang de l'harmonique considéré est très utile pour définir
les caractéristiques des filtres utilisés.
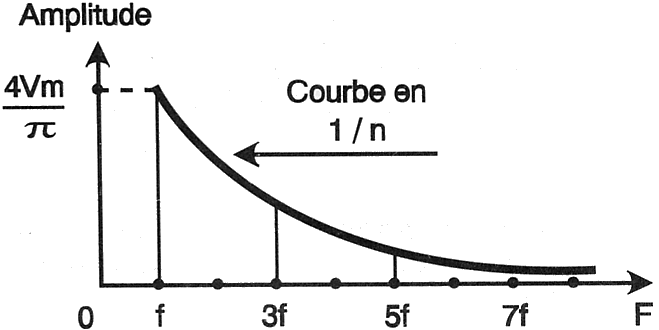
Figure
2 : Amplitude
du signal de la figure 1
On sait, par exemple, que les harmoniques
d'un signal carré ont des amplitudes qui varient en 1/n alors que celles d'un
signal triangulaire varient en 1/n². II résulte de cette propriété qu'un
amplificateur destiné à transmettre des signaux carrés devra avoir une bande
passante plus large que pour des signaux triangulaires, l'amplitude des
harmoniques de rang élevé étant plus faible (donc négligeable) avec des signaux
triangulaires qu’avec des signaux carrés.
2° Spectre d’un signal apériodique :
On trouve dans cette classification tous les
signaux non périodiques dont les plus représentatifs, surtout en ce qui
concerne le domaine électronique, sont l'impulsion, l'échelon et la rampe. La
figure 3 donne la représentation en fonction du temps de ces trois signaux que
l'on utilise couramment pour étudier la réponse des systèmes électroniques,
qu'il s'agisse d'asservissements ou plus simplement d'amplificateurs.

Figure
3 : Représentation
en fonction du temps
Pour
de tels signaux v(t), et à condition qu'ils soient d'amplitude finie et
d'intégrale finie sur l'intervalle de moins l'infini à plus l'infini,
si ceux-ci possèdent un nombre fini d'extréma et de discontinuités, il est
possible de définir non plus une série de Fourier.
L’expression v(t) est la transformée de
Fourrier de la fonction v(t) que l’on appelle aussi "densité spectrale de
v(f)". Cette grandeur étant généralement une fonction complexe puisque la
variable "j" figure dans le terme exponentiel, il est courant de ne
considérer que le module de V(f), que nous noterons 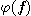 ,
qui représente la densité spectrale d'amplitude de v(t). ,
qui représente la densité spectrale d'amplitude de v(t).
La figure 4 donne le résultat des calculs
concernant le signal de la figure 4a qui est un créneau d'amplitude unitaire
apparaissant entre les instants -T et T, la figure 4b représente la densité
spectrale d'amplitude de ce même signal. Contrairement aux signaux périodiques,
le spectre est continu, toutes les fréquences sont présentes. Le calcul montre
que pour ce type de signal la courbe enveloppe définissant la densité spectrale
de chaque raie est une fonction en (sin X)
/ X.
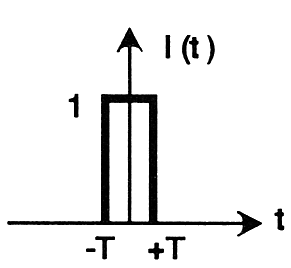
Figure
4a : Impulsion
unitaire
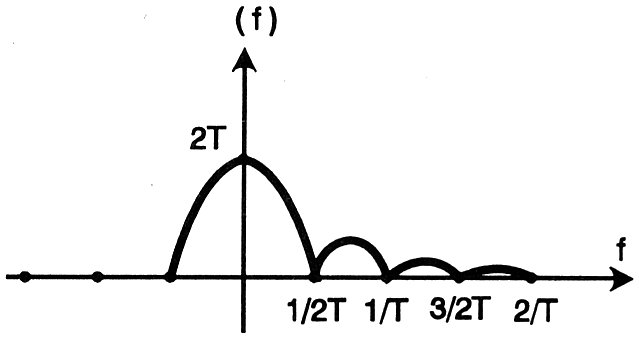
Figure
4b : Densité
spectrale d'amplitude de m'impulsion unitaire
Nous avons tenu à introduire ces points
particuliers afin que le lecteur soit conscient des différentes
caractéristiques qui existent entre les spectres des signaux périodiques et
apériodiques, ces notions n'étant que très rarement abordées, car elles
nécessitent des développements mathématiques assez conséquents qui sortiraient
du cadre de la revue.
II-
Rôle et caractéristiques d'un filtre :
1° Rôle :
Le
rôle essentiel d'un filtre consiste à modifier le spectre des signaux qui vont
y transiter afin d'obtenir des caractéristiques particulières. Citons, par
exemple, le cas des filtres qualifiés de correcteurs, qui amplifient les
signaux de fréquences basses et laissent passer les signaux de fréquences
élevées sans les modifier, afin de pallier à la déficience des haut-parleurs
dans le domaine des basses fréquences.
Bien
que le filtrage concerne principalement l'amplitude des signaux, les filtres ne
se contentent pas d'agir sur l'amplitude des signaux, leur action s'exerce
aussi sur la phase. Si l'on n'y prend pas garde, cette seconde action peut être
catastrophique sur le plan des résultats obtenus, comme nous le verrons un peu
plus loin dans cet exposé.
C'est
pour cette raison qu'un filtre doit être caractérisé par deux courbes représentant
respectivement l'action du filtre sur l'amplitude et sur la phase des signaux.
2° Caractéristiques :
Le
signal d'entrée ve(t) du filtre de la figure 5 est supposé sinusoïdal. Son
expression mathématique est ve(t) = Ve sin wt = Ve . sin (6,28 f). Le
signal présent à la sortie du filtre est
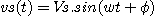 .
Le filtre ne modifiant pas la fréquence du signal, ve et vs ont la même
pulsation w = 6,28 f. .
Le filtre ne modifiant pas la fréquence du signal, ve et vs ont la même
pulsation w = 6,28 f.
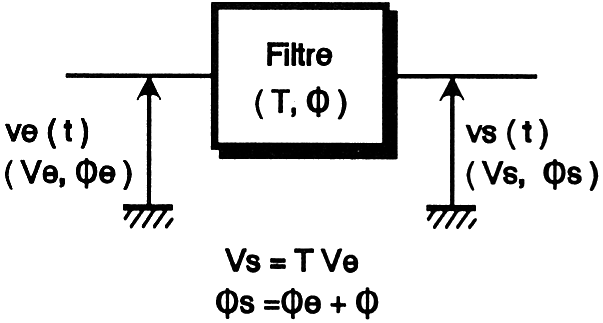
Figure
5 : Fonctions
d'un filtre en entrée - sortie
En
revanche, l'amplitude Ve est devenue Vs, et la phase (wt) de ve à l'instant « t
» est devenue
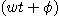 , du fait du passage du
signal dans le filtre. , du fait du passage du
signal dans le filtre.
Pour
caractériser l'effet du filtre sur le signal de fréquence f, on s'intéresse au
rapport des amplitudes des signaux vs(t) et ve(t) que l'on note |T| = Vs/Ve,
qui est un nombre sans dimension.
Comme
ce rapport varie avec la fréquence, on le note parfois |T (f)| ou |T(w)|.
En
ce qui concerne l'effet du filtre sur la phase des signaux, celle-ci est
caractérisée par la différence de phase existant entre vs(t) et ve(t) à un même
instant. On note cet effet par 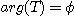 (lire argument),
quantité qui dépend elle aussi de la fréquence f. L'association des deux
grandeurs |T| et (lire argument),
quantité qui dépend elle aussi de la fréquence f. L'association des deux
grandeurs |T| et 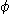 , que l'on note , que l'on note 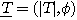 , est appelée fonction de transfert du
filtre. Dans de nombreuses situations, il est intéressant de faire appel à la
notion de gain définit par : G = 20 log (|T|). Celui-ci s'exprime en décibels,
dB en abrégé. , est appelée fonction de transfert du
filtre. Dans de nombreuses situations, il est intéressant de faire appel à la
notion de gain définit par : G = 20 log (|T|). Celui-ci s'exprime en décibels,
dB en abrégé.
Afin
de préciser le comportement des filtres en fonction de la fréquence, plusieurs
représentations auxquelles on donne le nom de diagrammes sont à la disposition
des utilisateurs.
Diagramme de Bode
:
II
s'agit de la courbe qui représente les variations du gain du filtre (ou de tout
montage en général) en fonction de la fréquence ou de la pulsation.
On
note cette fonction G = h(f). La figure 6b correspond à celui du filtre R-C de
la figure 6a. Généralement, le domaine dans lequel le filtre doit agir étant
assez important, on utilise pour les fréquences une échelle logarithmique. Ce
choix permet de condenser les résultats mais aussi de ne laisser aucun domaine
dans l'oubli, ce qu'une échelle linéaire ne permettrait pas.

Figure
6a : Filtre
passe-bas à éléments
RC
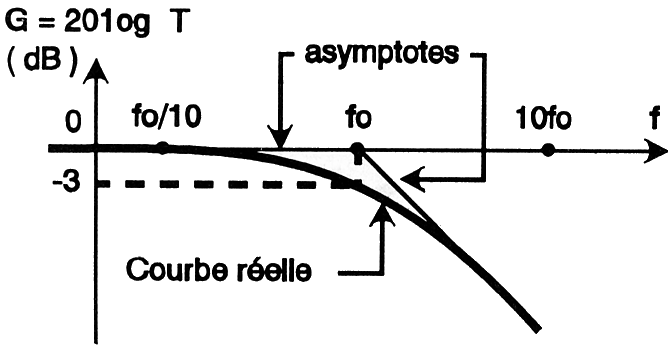
Figure
6b : Diagramme
de bode du gain
On
remarque que la courbe obtenue peut être approximée par deux droites que l'on
appelle des asymptotes. Leur point de concours correspond à la fréquence de
coupure "fo" du filtre. C'est pour cette fréquence que la courbe réelle du
filtre est la plus éloignée de ces asymptotes, l'écart vaut ici
- 3 dB. La
forme de la courbe renseigne de façon évidente sur les caractéristiques du
filtre.
On
note sur la figure 6b que les fréquences élevées sont atténuées (G donc |T|
diminue), alors que pour les fréquences basses, G = 0 dB, ce qui signifie que
les amplitudes de ve et de vs sont égales, donc que les signaux ne subissent
aucune modification pour ces fréquences. Nous sommes en présence d'un filtre
passe-bas.
Diagramme de Bode de la phase
II
s'agit, toujours pour le même filtre de la courbe qui donne les variations de (F
en fonction de f (ou w). L'échelle des fréquences
est encore logarithmique (pour les mêmes raisons). La figure 6c montre que pour
les fréquences basses, le déphasage introduit par le filtre est nul, qu'il tend
vers
(- 90°) quand f augmente.
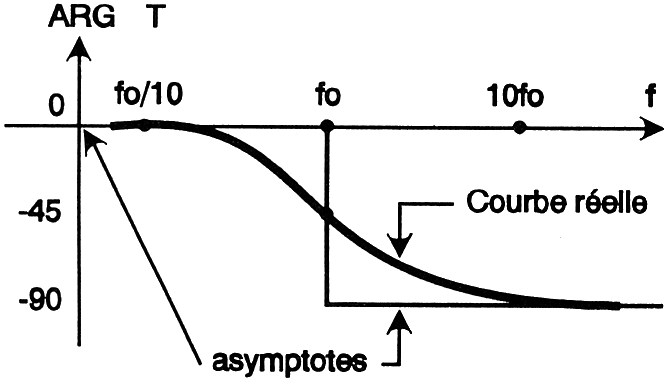
Figure
6c : Diagramme
de bode de la phase
On
remarque, ici encore, qu'il est possible de tracer des asymptotes qui rendent
compte du comportement du filtre de façon grossière, mais assez explicite
toutefois, tant pour les fréquences basses que pour les plus élevées. Pour la
fréquence de coupure fo, le déphasage introduit par le filtre étudié vaut -
45°.
Grâce
aux diagrammes de Bode dont nous venons de vous donner un exemple succinct, il
est possible de connaître avec précision l'action du filtre sur les différents
signaux qu'il sera amené à traiter.
Diagramme de Black
La
figure 6d propose celui-ci toujours pour le filtre de la figure 6a. Pour le
tracer, on représente pour chaque fréquence la valeur du gain G du filtre en
fonction du déphasage  qu'il introduit à cette même
fréquence. Bien qu'une seule et même courbe soit suffisante pour disposer
simultanément de la valeur du gain et de la phase, l'interprétation est moins
aisée qu'avec les diagrammes de Bode. qu'il introduit à cette même
fréquence. Bien qu'une seule et même courbe soit suffisante pour disposer
simultanément de la valeur du gain et de la phase, l'interprétation est moins
aisée qu'avec les diagrammes de Bode.
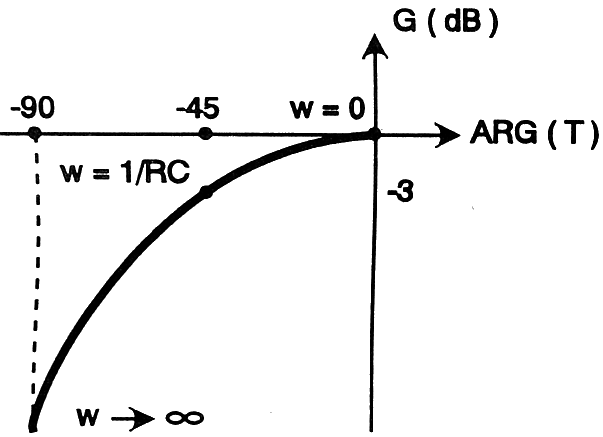
Figure
6d : Diagramme
de Black
Diagramme de Nyquist
La
notation mathématique 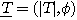 que nous avons utilisée
pour la fonction de transfert du filtre peut s'interpréter comme un vecteur
dont |T| représente la longueur et ( que nous avons utilisée
pour la fonction de transfert du filtre peut s'interpréter comme un vecteur
dont |T| représente la longueur et (
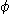 l'angle existant entre ce
vecteur et l'axe horizontal qui sert de référence (fig. 7). Pour chaque valeur
de la fréquence, la longueur et la position du vecteur se modifient. Si l'on
joint les extrémités de tous les vecteurs représentatifs de T, on
obtient une courbe que l'on appelle diagramme de Nyquist. Pour s'y retrouver,
il faut que le diagramme soit gradué en fréquence (fig.6e). l'angle existant entre ce
vecteur et l'axe horizontal qui sert de référence (fig. 7). Pour chaque valeur
de la fréquence, la longueur et la position du vecteur se modifient. Si l'on
joint les extrémités de tous les vecteurs représentatifs de T, on
obtient une courbe que l'on appelle diagramme de Nyquist. Pour s'y retrouver,
il faut que le diagramme soit gradué en fréquence (fig.6e).
Comme
pour le diagramme de Black, celui de Nyquist fournit sur une seule
représentation les valeurs du module et de la phase de T.
Certains vont se demander à quoi peuvent bien servir ces
diverses représentations qui n'apportent en apparence pas plus de
renseignements l'une que l'autre.
Suivant le domaine d'application, certains diagrammes sont
plus commodes à employer que les autres, aussi devra-t-on connaître chacun et
utiliser le plus approprié suivant l'application envisagée.
En
ce qui concerne le filtrage proprement dit, nous utiliserons essentiellement
les diagrammes de Bode qui, par leurs formes (surtout celle du gain), indique
immédiatement la nature du filtre avec lequel on est confronté.

Figure
6e : Diagramme
de Nyquist
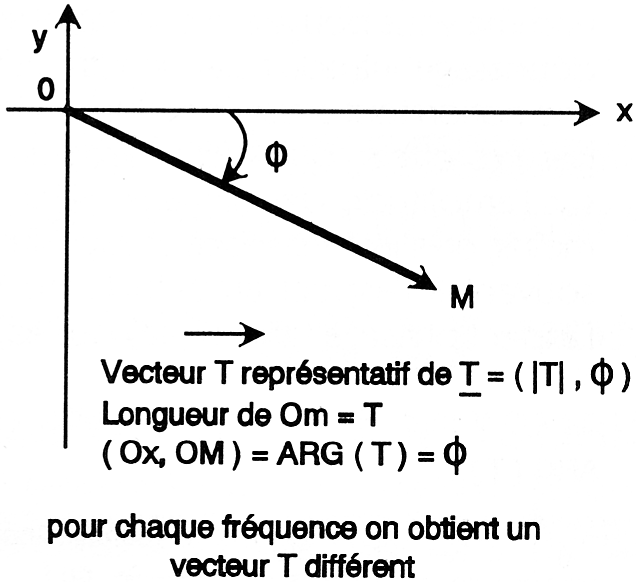
Figure
7 : L'angle
de phase
3° Importance du déphasage
En
partant de l'expression 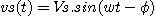 qui représente la tension de sortie d'un circuit électrique quelconque,
expression que l'on peut aussi mettre sous la forme
qui représente la tension de sortie d'un circuit électrique quelconque,
expression que l'on peut aussi mettre sous la forme 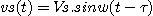 avec
avec 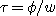 ,
nous voyons qu'un signal de fréquence f qui traverse un circuit électrique sort
de celui-ci avec un retard de valeur ,
nous voyons qu'un signal de fréquence f qui traverse un circuit électrique sort
de celui-ci avec un retard de valeur 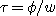 qui dépend de la pulsation w du signal.
qui dépend de la pulsation w du signal.
Si
nous supposons maintenant que deux signaux de fréquences f1, et f2 (pulsations
respectives wl et w2) sont appliqués simultanément à l'entrée de ce même étage,
il est évident que les temps de transit respectifs seront 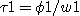 et et 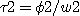 . .
Réfléchissons
un instant et posons-nous la question de savoir ce qui se passerait si les
temps de transit 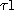 , et , et 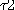 étaient différents. Pour aider à la compréhension du phénomène, nous pouvons
imaginer que deux instruments de musique émettent simultanément deux notes
formant un accord.
étaient différents. Pour aider à la compréhension du phénomène, nous pouvons
imaginer que deux instruments de musique émettent simultanément deux notes
formant un accord.
L'inégalité
des durées 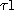 et et 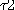 correspondrait à la sortie des notes à des instants différents, ce qui, avouons
le, risquerait de donner une belle cacophonie et n'est pas le but recherché.
correspondrait à la sortie des notes à des instants différents, ce qui, avouons
le, risquerait de donner une belle cacophonie et n'est pas le but recherché.
Afin
d'assurer un temps de transit identique pour toutes les fréquences, il faut
respecter la condition 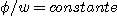 . Cette condition impose que la courbe . Cette condition impose que la courbe 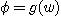 soit une droite comme celle de la figure 8
(l'échelle utilisée pour les fréquences doit être linéaire). Les filtres ou,
plus généralement, les montages qui vérifient cette condition sont qualifiés de
montages à phase linéaire. soit une droite comme celle de la figure 8
(l'échelle utilisée pour les fréquences doit être linéaire). Les filtres ou,
plus généralement, les montages qui vérifient cette condition sont qualifiés de
montages à phase linéaire.

Figure
8 : Filtre
à phase linéaire
II
est évident que les amplificateurs HiFi doivent posséder cette propriété, sinon
ils introduisent ce que l'on nomme de la distorsion de phase.
Comme
vous pouvez le constater, le déphasage introduit par un filtre est une notion
tout aussi importante, de par ces effets, que celle introduite sur l'amplitude
des signaux. Néanmoins, on s'intéresse beaucoup plus souvent à l'aspect
amplitude qu'à l'aspect phase, attitude que nous essayerons de corriger quand
nous aborderons l'étude détaillée des filtres.
Maintenant
que nous connaissons les effets des filtres sur les signaux, nous allons vous
présenter les différents types de filtres.
III-
Les différents types de filtres:
La
diversité des filtres, de leur domaines d'application, de leurs performances
sont autant de facteurs qui font qu'il n'est pas possible de donner une seule
classification pour ceux-ci.
Classement
suivant l'action sur le spectre :
On
peut effectivement classer les filtres suivant leur façon d'agir sur un domaine
particulier de fréquences. On rencontre ainsi quatre structures fondamentales:
les filtres de type passe-bas, passe-haut, passe-bande ou réjecteur dont le nom
est suffisamment évocateur pour qu'on en comprenne le sens. L'allure des courbes
de gains de ces filtres est donnée à la figure 9
(a,b,c,d).
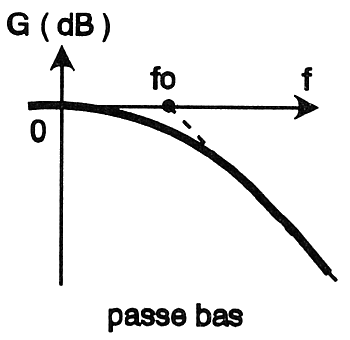
Figure
9a : Le filtre
passe-bas
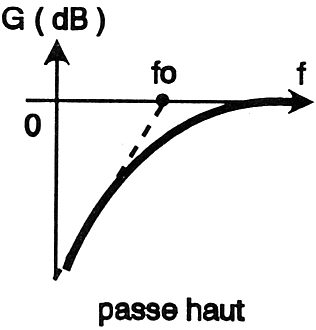
Figure
9b : Le filtre
passe-haut
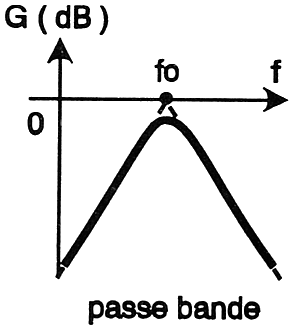
Filtre
9c : Le filtre
passe bande

Figure
9d : Le filtre
réjecteur
Classement
suivant l'efficacité :
On
peut classer les filtres suivant leur "force", car il n'existe pas un
seul type de filtre passe-bas mais plusieurs, auxquels on attribue un "ordre" d'autant plus élevé que leur atténuation dans la zone atténuée est
plus importante (et (ou) plus rapide). Cette remarque vaut aussi pour les
passe-haut, passe-bande et réjecteurs.
On
trouve donc des filtres d'ordre 1, 2 et même beaucoup plus (3... 7, 9, etc.).
La figure 10 donne l'aspect de la courbe de gain des filtres passe-bas d'ordre
1, 2, 3.

Figure
10 : Filtre
passe-bas d'ordres différent
Classement
suivant le matériel utilisé :
On appelle filtre passif, un filtre dans lequel
n'interviennent que des composants R, L, C. Pour ceux qui utilisent des AOP ou
des transistors, on les qualifie de filtres actifs.
Les
filtres passifs sont utilisés aussi bien en BF (filtres pour enceintes
acoustiques, par exemple) qu'en HF (passe-bande en général). L'avantage de ces
filtres est qu'ils sont rarement limités au niveau de l'amplitude des signaux
traités, ce qui n'est pas le cas des filtres actifs.
Le
domaine d'activité des filtres actifs, qui se sont énormément développés avec
l'utilisation des AOP, va du continu à plusieurs mégahertz. De nombreuses
familles de filtres aux propriétés multiples et variées sont apparues grâce aux
AOP.
Classement
suivant le domaine d'application :
En
HiFi, on trouve les correcteurs, les égaliseurs dont la technologie fait
généralement intervenir des AOP et qui, de ce fait, en font des filtres actifs.
Pour
ce qui concerne les asservissements, les filtres utilisés ont pour rôle
d'améliorer la précision et (ou) la stabilité, d'où leur nom de correcteurs.
En
domotique, les filtres sont tout aussi présents que dans les autres domaines
puisqu'on rencontre ceux-ci sur les lignes d'alimentation des variateurs
électroniques de vitesse ou sur celles des gradateurs pour l'éclairage. Dans
ces applications, on s'arrange généralement pour éliminer les harmoniques dus
aux découpages des sinusoïdes secteur.
En
HF, et en particulier pour les émetteurs dont la puissance commence à devenir
importante, on utilise fréquemment des filtres réjecteurs destinés à supprimer
d'éventuels harmoniques dont la présence pourrait perturber une bande de
fréquence sur laquelle l'émetteur ne doit absolument pas se trouver.
Ce
classement, qui permet en fait de répertorier les domaines d'application des
filtres, n'est qu'indicatif, mais suffisamment évocateur pour qu'on entrevoit
l'intérêt que présente ce domaine particulier de l'électronique.
Les
filtres numériques que l'on rencontre de plus en plus fréquemment dans les
nouveaux systèmes comme les lecteurs de CD feront l'objet d'un article.
Article tiré de la revue
Electronique Pratique Novembre 1994. Auteur : F. JONGBLOET.
|