|
Article tiré de la revue
Elektor n°191 - Mai 1994. Auteur : inconnu !
Sommaire
:
Introduction
:
Résistance
thermique :
Résistances
- séries :
Directives
et informations :
Application
pratique de la théorie :
Sécurité
de contact & isolation :
La
montage :
Epilogue
:él

Introduction :
Les probabilités que tous ceux
d'entre nos lecteurs ayant, par le passé, réalisé, qui une alimentation, qui un
amplificateur de puissance, aient été confrontés à ce problème sont grandes ! Dans
l'étage de sortie d'un tel montage une bonne partie de la puissance se transforme en
chaleur. Pour permettre aux composants en question de se débarrasser facilement de cette
chaleur, on fait appel, en règle générale à un, voire plusieurs, radiateurs.
Nous nous proposons, dans cet article,
de porter notre attention sur certaines informations de base qui vous permettront, à
l'avenir, de (mieux ?) déterminer quel radiateur utiliser en fonction de l'application
concernée.
Aux yeux du profane un "
électronicien " est bien souvent une sorte de professeur Tournesol, un bricoleur
quelque peu désincarné qui, de temps en temps, réalise un montage pour passer ensuite
la quasi-totalité de son temps libre à la recherche des erreurs qu'il comporte. II
semble que dans le monde de l'électronique - tout comme cela est devenu le cas plus
récemment dans celui des micro-ordinateurs - il y ait toujours quelque chose qui ne
fonctionne pas correctement.
Nous n'allons pas perdre notre temps
à polémiquer sur la véracité ou non de cette description. II est vrai cependant que
les activités de l'électronicien " lambda " sont d'une variété sensiblement
plus grande. II passe son temps non seulement à la réalisation du circuit électronique,
mais aussi à sa mise en boîtier, son câblage et la prise de précautions permettant le
refroidissement de certains des semi-conducteurs qu'il comporte. Cette dernière activité
est souvent sous-estimée par le petit monde des électroniciens, tant amateurs que
professionnels ! Pourquoi se faire du souci ? Le type de radiateur requis fait partie
de la liste des composants, n'est-ce pas. Sinon, il suffit de prendre un exemplaire à
l'aspect physique similaire à celui visible sur les photos illustrant l'article ?!
II nous semble parfaitement superflu
d'attirer l'attention de notre " honorable " lecteur sur le fait qu'une telle
attitude est à la fois partisane du moindre effort et potentiellement dangereuse. Tout
concepteur de réalisations personnelles se doit de choisir le radiateur répondant aux
exigences spécifiques du circuit en question. On pourrait, pour " mettre toutes les
chances de son côté ", envisager de faire appel au plus grand radiateur disponible.
Cette " solution " garantira (fort probablement) un refroidissement adéquat,
mais il ne faudra pas oublier qu'un radiateur de dimensions importantes coûte
relativement cher et interdit la réalisation d'un circuit aux dimensions les plus
compactes possible.
II faut, pour bien comprendre les
circuits électroniques, disposer de certaines connaissances de base; il en va de même
pour une utilisation " correcte " des radiateurs. C'est très exactement pour
cette raison que nous allons essayer de sortir la théorie des radiateurs de sa "
préhistoire ", espérant qu'après la lecture de cet article vous serez en mesure de
déterminer, pour n'importe quelle application, le radiateur à utiliser.
Résistance thermique :
C'est avec ces 2 termes que commence
notre récit historique concernant les radiateurs. Pour bien comprendre ce qu'est, en
fait, la résistance thermique, nous allons commencer par nous intéresser à la loi d'un
certain monsieur Ohm. La formule énoncée par Ohm, U = I x R, correspond grossièrement
à la formule utilisée pour les calculs thermiques.
La figure
1 montre une résistance ayant une valeur R. La différence
de tension. DU, aux bornes de cette résistance est égale à
la différence entre les niveaux de tensions avant et après cette résistance, ce qui
mathématiquement s'exprime par la formule U1 - U2. En faisant appel à la loi d'Ohm nous
pouvons calculer l'intensité I du courant traversant la résistance : I = DU / R. La valeur R de la résistance correspond donc à DU / I .
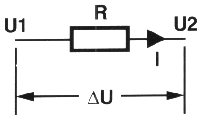
Figure 1: II
est relativement simple de passer de la loi d'Ohm
standard à sa variante thermique.
Après avoir disséqué le substantif
résistance, intéressons-nous maintenant à l'adjectif thermique.
II est également possible, dans le
cas de la théorie thermique, de formuler une variété de la loi d'Ohm dans laquelle on
remplace la différence en tension DU par la différence en
température DT (qui correspond, bien entendu à T1 -T2).
L'unité que l'on utilise en règle générale pour exprimer la température est le degré
Kelvin (K). La seule différence entre une température exprimée en degrés Kelvin et son
équivalent donné en degrés centigrades (ou degrés Celsius) est un décalage d'échelle
de 273°. Zéro degré centigrade correspond donc à 273°K. S'il s'agit de déterminer
une différence en température l'unité (K ou °C) utilisée ne joue aucun rôle, le
résultat de la soustraction sera toujours le même. Prenons, à titre d'exemple, une
température T2 de 10°C et une température T1 de 25°C.
La différence entre ces deux
températures est alors de 25 -10 = 15°C. Exprimé en degrés Kelvin le calcul de D T se fait de la manière suivante : (273 + 25)°K - (273 +
10)°K et le résultat est identique à la soustraction en degrés centigrades : 15°K.
La résistance électrique R de la loi
d'Ohm est remplacée par sa version thermique baptisée Rth (figure
2). La valeur de Rth détermine l'importance du flux
thermique à travers cette résistance. Ce flux thermique s'exprime en une quantité de
puissance P à transformer en chaleur. À l'image de la loi électrique d'Ohm, on se
retrouve donc avec une formule quasi identique Rth= DT/ P. II
ne nous faut pratiquement rien de plus, outre cette formule, pour déterminer le radiateur
à utiliser.
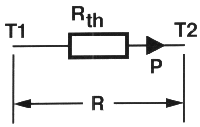
Figure 2:
Dans le cas de la " loi d'Ohm thermique" il se produit, suite au flux thermique
P à travers la résistance Rtn, une différence en température aux bornes de Rth avec
une valeur de DT.
Nous avons besoin, pour vous donner
une idée de la forme dans laquelle on retrouve ces trois facteurs dans la vie pratique,
du croquis de la figure 3. Cette figure nous montre un espace clos que l'on pourra
comparer à une salle de séjour. À l'intérieur de ce volume se trouve un appareil de
chauffage quelconque qui porte le volume de la pièce à une température : T1. À
l'extérieur de cet espace il règne une autre température : T2.

Figure 3: Si
un espace clos est chauffé à une température T1, il se produit un flux thermique
de l'intérieur vers l'extérieur, à condition cependant que la température extérieure
T2
soit inférieure à T1. La résistance thermique Rth des murs détermine la valeur de la
perte en puissance P.
À condition que nous connaissions la
résistance thermique, Rth, des murs, nous pouvons calculer la perte de puissance
thermique au travers des dits murs. Un mur bien isolé possède une résistance thermique
élevée ce qui se traduit (P = DT / Rth rappelez-vous) par une
perte de puissance (chaleur) vers l'extérieur moindre. Si DT
est nulle (DT=0), la loi " thermique " d'Ohm nous
porte à conclure qu'il n'y a pas de perte thermique. Le fait que DT
= 0 signifie tout simplement que la température intérieure est égale à la température
extérieure.
On notera qu'un mur n'est pas
forcément fait d'un seul type de matériau. Dans la pratique les murs extérieurs d'une
maison sont souvent du type creux (figure 4). Un mur creux se compose, par exemple, de deux murs en briques, espacés
de quelque 5 cm l'un de l'autre. Actuellement l'espace entre les deux murs est rempli avec
un matériau isolant. On comprendra sans doute que la résistance thermique d'un mur creux
isolé se compose en fait d'une mise en série de plusieurs résistances thermiques
distinctes (figure 5). Pour
déterminer la résistance thermique totale du mur, il suffit donc d'additionner ces
différentes résistances thermiques mises en série.
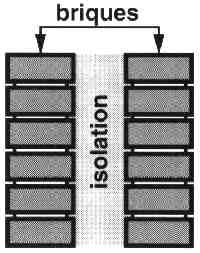
Figure 4:
Dans la pratique, la résistance thermique d'un mur (creux)
se compose de plusieurs résistances thermiques distinctes.
Dans cet exemple relativement simple, nous voyons déjà une mise
en série de deux résistances thermiques " briques " et une résistance
thermique " isolation ".

Figure 5: II
suffit d'additionner toutes les résistances thermiques
distinctes pour obtenir la résistance thermique totale.
Nous voici arrivés à la fin de la
petite excursion - instructive, nous l'espérons - dans le monde du bâtiment. II est
temps maintenant de nous intéresser au refroidissement de semi-conducteurs.
Résistances-série :
Dans les paragraphes précédents nous
avons vu que la résistance thermique peut prendre la forme d'une mise en série de
plusieurs résistances thermiques, propres aux différents matériaux utilisés. C'est
très exactement le cas lorsque l'on monte un semi-conducteur sur un radiateur. Avant
d'examiner de plus près la technique de montage, nous allons nous intéresser d'abord aux
différentes résistances thermiques qui entrent en ligne de compte dans le cas d'un tel
assemblage.
Lors des explications à suivre il
nous faudra inévitablement utiliser diverses dénominations (ou abréviations, que l'on
retrouve d'ailleurs dans la quasi-totalité des fiches techniques fournies par les
fabricants de semi-conducteurs) anglaises pour indiquer chacune des résistances
thermiques.
La figure
6 montre un transistor de puissance, une plaquette
d'isolation et un radiateur. La disposition des différents composants et leur espacement
ne correspondent pas à la réalité; ces éléments ont été " éclatés "
pour faciliter la compréhension du schéma et de ce qui s'y rapporte.

Figure 6: Le
montage d'un transistor sur un radiateur
résulte en une mise en série de trois résistances thermiques.
Commençons avec le matériau
semi-conducteur à l'intérieur du transistor, car c'est très précisément à cet
endroit que la puissance électrique est transformée en chaleur. Cette température
s'appelle junction temperature (température de jonction). Le mot junction se
rapporte aux jonctions qui existent entre les différentes couches de silicium (telles que
P-N-P d'un transistor PNP par exemple).
La première résistance thermique, à
savoir (Rth j-mb), se trouve entre la jonction (j) et le boîtier (mb = mountingbase) du
transistor. La seconde résistance thermique, Rth mb-h, est celle qui existe entre le
boîtier du composant et le radiateur (h = heatsink). Sa valeur dépend de
l'absence ou de la présence d'un isolant (plaquette, pâte thermoconductrice) entre le
composant et le radiateur et, bien entendu, du matériau dont est fait l'isolant en
question. II existe, pour finir, une troisième résistance thermique, celle présente
entre le radiateur et son environnement (a = ambient) résistance qui s'appelle
Rth h-a.
La figure
7 représente l'ensemble des différentes résistances
thermiques, une source de température, Tj-Ta et le flux de la chaleur P.

Figure 7:
Schéma thermique d'un transistor monté sur un radiateur.
Nous allons partir à la recherche des valeurs exactes des différents facteurs.
Dans le paragraphe à suivre nous
allons voir où l'on pourra trouver les données concernant les résistances thermiques
mentionnées.
Directives et informations :
Maintenant que l'on sait de quelles
informations il faudra disposer pour déterminer la résistance thermique totale il serait
utile de savoir aussi où on peut les trouver.
Commençons au point le plus chaud de
la chaîne : le semi-conducteur. Parmi les données mentionnées dans les fiches
techniques des transistors figurent, en général, plusieurs résistances thermiques. Le tableau 1 donne un certain nombre de valeurs
de résistances thermiques, exprimées en degré par watt (°C/W) pour les boîtiers de
semi-conducteur les plus courants.
Tableau 1: Résistances thermiques pour les
boîtiers T0. |
| Boîtier |
Rth j-a (°C/W) |
Rth j-mb (°C/W) |
| TO-18 |
500 |
200 |
| TO-92 |
250 |
150 |
| TO-39 |
200 |
12,5 |
| TO-126 |
100 |
5 |
| TO-220 |
70 |
2 |
| TO-3 |
40 |
1,5 |
Dans ce tableau, Rth j-a indique la
valeur de la résistance thermique qui existe entre le semi-conducteur et son
environnement. Cette valeur n'est utilisable que si l'on monte le composant en question
sans radiateur. Pour tout calcul avec radiateur, il nous faut la valeur de la
résistance thermique existant entre le boîtier du composant et le radiateur. Nous avons
trouvé donc la première résistance thermique.
II existe cependant une autre donnée
du semi-conducteur dont on aura besoin : la température maximale admissible par le dit
semi-conducteur, Tj. En règle générale cette donnée fait partie des informations
fournies dans les recueils de caractéristiques (databook) des différents fabricants. La
valeur de Tj, ne dépasse pratiquement jamais les 200°C.
La résistance Rth mb-h (existant
entre le boîtier du composant et le radiateur) dépend de la technique de montage mise en
ouvre. Autrement dit : cette résistance est fonction du matériau intercalé entre
le boîtier du composant et le radiateur.
Le tableau
2 propose quelques possibilités de montage et indique la
résistance thermique en résultant.
| Tableau 2: Techniques de montage et leur Rth
mb-h. |
|
|
Rth
mb-h |
| Sans
plaquette d'isolation et sans pâte thermoconductrice |
0,05 à
0,2 |
| Sans
plaquette d'isolation et avec pâte thermoconductrice |
0,005 à
0,1 |
| Plaquette en oxyde d'aluminium avec pâte thermoconductrice |
0,2 à 0,6 |
| Plaquette en mica (0,05 mm) avec pâte thermoconductrice |
0,4 à 0,9 |
| Plaquette
en silicone sans pâte thermoconductrice |
0,84 à
0,88 |
Si l'on se décide à monter le
composant directement sur le radiateur, cette résistance thermique est relativement
faible (métal contre métal) et le fait de doter l'ensemble d'un rien de pâte
thermoconductrice réduit d'avantage cette valeur (déjà relativement bonne).
S'il est requis de monter le
composant de façon isolée, on a plusieurs possibilités. II existe des plaquettes
d'isolation de matériaux différents, tels que mica, silicone ou autre oxyde d'aluminium
(céramique). II suffit de regarder le tableau 2 pour découvrir que l'oxyde d'aluminium possède la résistance thermique
la plus faible et que la plaquette en silicone constitue en fait le choix le moins
favorable (résistance thermique la plus élevée). Dans l'un de paragraphes suivants nous
allons regarder en détail les différents avantages et inconvénients de ces matériaux.
II nous manque encore une
résistance thermique : celle qui existe entre le radiateur et son environnement, Rth n-a.
Pour cette valeur il faudra se référer directement aux données fournies par le
fabricant du radiateur en question. La résistance thermique mentionnée (exprimée en
°C/W ou en 'K/W, ces 2 unités étant identiques) dans les fiches techniques n'est
valable que pour un radiateur noir dont les ailettes de refroidissement ont disposées
verticalement (circulation d'air par convexion). Le tableau 3 montre l'évolution de la valeur de
Rth h-a dans des conditions moins favorables.
| Tableau 3: Adaptation de Rth h-a dans des
conditions moins bonnes |
|
|
Rth h-a |
| Radiateur en aluminium
de couleur "naturelle" |
Rth h-a +10 à 15% |
| Disposition
horizontale des ailettes de refroidissement |
Rth h-a +15 à 20% |
Et si nous
poursuivions notre étude des radiateurs en procédant, à titre d'exemple pratique, au
calcul d'un radiateur pour une application donnée. Nous passerons en revue, à la suite
de ce paragraphe consacré aux chiffres, un certain nombre de techniques de montage et de
types de radiateurs.
Application pratique de la théorie :
Imaginez-vous une situation
parfaitement possible en pratique.
Nous allons prendre un transistor de
puissance à boîtier TO-3. Dans cet exemple de calculs tiré de la pratique nous aurions
tout aussi bien pu prendre un régulateur de tension.
Dans cet exemple il existe, aux bornes
de la jonction émetteur collecteur, une tension de 20 V. Le courant d'émetteur
traversant le transistor en présence d'une telle tension est de 3 A. La puissance P à
transformer en chaleur est donc de 3 A x 20 V = 60 W. Cette valeur est en fait la
première donnée que nous pouvons mettre dans le schéma de la figure 8, représentant le flux de chaleur.
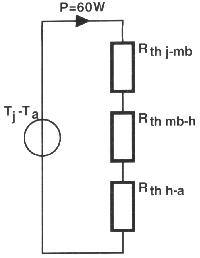
Figure 8: On
procède d'abord au calcul de la puissance P à transformer en chaleur.
Après avoir trouvé cette valeur on la mettra à sa place dans le schéma.
Les caractéristiques techniques des
semi-conducteurs nous apprennent que la température maximale du matériau
semi-conducteur, Tj, ne devrait pas dépasser 200°C en moyenne. II est important de
savoir que, dans ces conditions, on se met dans la situation la plus difficile
(worst-case). Si, dans la pratique, un semi-conducteur atteignait réellement une
température T, de 200°C, il existerait un grand danger de brûlure graves en cas
d'entrée en contact avec lui.
Dans le paragraphe à suivre nous
parlerons des différentes mesures de sécurité, la sécurité de contact y comprise.
En prenant pour la température
ambiante, Ta, une valeur " standard " de 25°C, la différence en température
Tj-Ta aura une valeur de 200°C - 25°C =175°C.
La figure
9 montre le schéma du flux calorifique, complété de cette
valeur.

Figure 9: La
valeur suivante (175°C) indique la différence entre
la température du semiconducteur et celle de l'environnement.
En étant arrivés à ce point, nous
pouvons dès à présent déterminer la résistance thermique totale en faisant appel à
la " loi d'Ohm thermique ".
L'utilisation de cette formule nous
apprend que Rth totale, est identique à DT/P = 175°C/60 W =
2,92°C/W (= 2,92°K/W). La somme de toutes les résistances thermiques se doit donc
d'être au pire égale, voire, de préférence, inférieure, à cette valeur. Pour pouvoir
répondre à cette exigence il nous faut commencer par connaître la valeur de chacune des
résistances thermiques. Ce n'est qu'ensuite que l'on pourra déterminer les
caractéristiques du radiateur à utiliser.
D'après le tableau 1 on pourra prendre, pour un
boîtier du type TO-3, une valeur de 1,5°C/W pour la résistance thermique Rth j-mb (voir
figure 10). Si l'on opte ensuite
pour la meilleure possibilité d'isolation (celle avec la résistance thermique la plus
faible donc) le tableau 2 nous apprend qu'il faudra prendre une plaquette en oxyde
d'aluminium dotée de pâte thermoconductrice. Dans ces conditions la résistance
thermique Rth mb-h aura, dans les conditions les moins favorables, une valeur de 0,6°C/W
(figure 11). Nous disposons
maintenant de toutes les valeurs requises pour pouvoir calculer la valeur de la
résistance thermique Rth h-a, du radiateur à utiliser.

Figure 10: La
valeur exacte de la résistance thermique existant entre le matériau
semiconducteur et le boîtier du composant dépend en fait du type de boîtier utilisé.
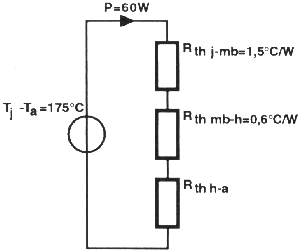
Figure 11: La
valeur de Rth mb h est fonction du matériau
qui se trouve entre le boîtier du semi-conducteur et le radiateur.
La résistance thermique totale étant
de 2,92°C/W (cf. plus haut), Rth h-a devra être égale ou inférieure à :
2,92°C/W - (1 ,5°C/W +
0,6°C/W) = 0,82°C/W.
La figure
12 montre un radiateur auquel on pourra faire appel. Il
s'agit d'un radiateur du type SK88 dont le croquis et le graphique donnent
toutes les caractéristiques techniques. La courbe du diagramme montre qu'un
radiateur SK88 avec une longueur de 125 mm possède une résistance thermique de
0,75°C/W. Le fait que cette valeur soit même légèrement inférieure à celle requise,
à savoir de 0,82°C/W, montre bien que le SK88 est parfaitement approprié pour notre
application (à condition bien entendu, primo, que le radiateur soit peint en noir (le
sombre dissipe mieux que le clair) et, secundo, qu'il soit monté de façon à ce que ses
ailettes de refroidissement soient disposées verticalement !).

Figure 12: La
courbe du diagramme montre qu'un radiateur avec une longueur de 125 mm
serait parfait pour le transistor de notre exemple. L'utilisation d'un tel radiateur
résultera
même en une résistance thermique plus favorable : le radiateur possède une Rth h-a de
0,75°C/W,
valeur plus faible que celle de 0,82°C/W que nous avions calculée.
Sécurité de contact & isolation :
Dans l'exemple pratique du dernier
paragraphe nous sommes partis de l'idée qu'il n'y a pas de mal à ce que le composant
atteigne sa température de jonction maximale de 200°C. II est plus judicieux, en
général, de respecter une marge de sécurité sensiblement plus importante. Une valeur
utilisable pour Tj, se situe normalement entre 100 et 150°C. Toutes les données de
l'exemple pratique nous permettent de calculer très précisément quelle température
atteindront le boîtier du composant et le radiateur.
Pour permettre une meilleure
compréhension des calculs à effectuer nous avons, en figure
13, redessiné le diagramme du flux de chaleur.

Figure 13:
Maintenant que l'on connaît tous les facteurs requis, il n'est plus sorcier
de calculer les températures que prendront le boîtier du semi-conducteur et le
radiateur.
La température du boîtier du
semi-conducteur est identique à Tj, diminuée de la différence en température qui
existe entre le matériau semi-conducteur et le boîtier (Rh j-mb). La " chute de
tension " aux bornes de la " résistance " Rth j-mb est identique à P (le
flux de chaleur) multiplié par la valeur de Rth j-mb. Le boîtier prendra donc une
température de :
Tj - P x Rth j-mb = 200°C - 60 W x
1,5°C/W = 110°C.
L'importance de cette valeur nous
apprend qu'il est dangereux donc de toucher au boîtier du semi-conducteur. II faudra en
conséquence, dans la pratique, monter ce composant d'une manière telle qu'il soit
impossible d'entrer " par hasard " en contact avec lui.
La température définitive du
radiateur sera inférieure de P x Rth mb-h, ou, dans le cas de notre exemple égale à :
110°C - 60 W x 0,6°C/W =
74°C.
La valeur relativement élevée de
cette température est un facteur à prendre en compte lors du dimensionnement du
radiateur.
II ne nous reste plus
qu'à voir jusqu'à quelle valeur la température ambiante, Ta, pourrait monter dans le
cas d'une température de jonction Tj de 200°C. Ta prendra une valeur égale à la valeur
de la température du radiateur diminuée de la différence en température existant entre
le radiateur et son environnement. Dans notre exemple Ta sera donc de :
74°C - 60 W x 0,75°C/W =
29°C.
Le " gain " de 4°C par
rapport à la température ambiante de 25°C de laquelle nous sommes partis est le
résultat de la résistance thermique plus faible du radiateur utilisé (0,75°C/W au lieu
de 0,82°C/W).
Lorsque l'on doit choisir un radiateur
il ne faudra pas oublier de tenir compte du fait que la température ambiante, Ta, peut
atteindre une valeur plus élevée (en été par exemple). Dans nos régions, on peut
estimer que la température ambiante maximale praticable est de l'ordre de 35°C.
En résumé, nous pouvons fournir
quelques valeurs directives pour les différentes températures. Pour des raisons de
sécurité - et pour éviter un décès prématuré du composant - il faudra limiter la
température maximale du semi-conducteur à une valeur comprise entre 100 et 150°C. Pour
éviter les dangers de brûlure en cas de contact, la température du radiateur ne devrait
pas dépasser une température égale à celle de la température ambiante + 30°C. Dans
le cas d'une température ambiante de 25°C le radiateur ne sera donc pas plus "
chaud " que 55°C.
Si, finalement,
on se sert de la valeur directive de 35°C comme température ambiante maximale, on aura
un refroidissement de semi-conducteur garanti fonctionnant sans le moindre problème.
Nous allons, après cette partie
purement théorique, voir quelles sont les possibilités de montage de semi-conducteurs
existant ainsi que leur mise en ouvre correcte.
La photo de la figure 14 montre les boîtiers de
semi-conducteurs les plus courants ainsi que leur code (nom) utilisé. Le tableau 1 donne
la résistance thermique Rth j-mb de tous ces boîtiers, exception faite du SOT-65. La
forme du boîtier, le nom et la résistance thermique des boîtiers de la figure 14 ne
changent pas, peu importe qu'il s'agisse d'un transistor ou d'un régulateur de tension.

Figure 14:
Vue générale des bottiers de semi-conducteurs
les plus courants avec leur dénomination.
Pour comprendre pourquoi, dans
certaines conditions, il est requis d'isoler le semi-conducteur électriquement du
radiateur il faudra regarder l'extrait d'un schéma d'un amplificateur de sortie de la figure 15. Les transistors de puissance
utilisés ont un boîtier du type TO3 qu'il faudra monter sur un radiateur. Pas de panique
jusqu'ici ! Tout change pourtant du simple fait que le collecteur d'un tel transistor de
sortie est relié à son boîtier métallique. Dans le cas des régulateurs de tension
l'une des broches est également relié à sa partie de fixation métallique. Un second
examen du schéma de la figure 15
nous apprend donc qu'on aura de gros problèmes dans le cas d'un montage non isolé des
deux transistors sur un radiateur commun. Dans ces conditions les collecteurs de deux
transistors seraient interconnectés et la tension d'alimentation positive serait
court-circuitée !!
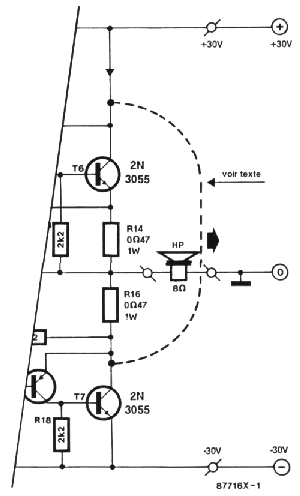
Figure 15: Ce
petit extrait d'un schéma d'un amplificateur de sortie servira à prouver pourquoi,
dans certaines conditions, il est important de monter les semi-conducteurs en les isolant
par rapport au radiateur.
Même dans le cas du montage sur un
radiateur d'un seul semi-conducteur, il peut être judicieux de l'isoler électriquement
du radiateur métallique. Ceci est très important si la partie de fixation du
semi-conducteur présente une tension dangereuse (> 42 V).
La photo de la figure 16 montre
différents matériaux d'isolation. Le tube (à gauche) contient la fameuse pâte
thermoconductrice servant à améliorer sensiblement le transfert de chaleur du boîtier
du semi-conducteur, à travers la plaquette d'isolation, au radiateur. Les plaquettes
blanches sont faites d'un matériau céramique à base d'oxyde d'aluminium et se
caractérisent par une résistance thermique très faible (tableau
2). II est préférable, quelles que soient les conditions,
de faire appel à ce genre de plaquettes d'isolation. Les plaquettes quasi-transparentes
existent depuis un bon nombre d'années. II s'agit de plaquettes en mica qui ont une
résistance thermique relativement bonne. La plaquette grise finalement est faite d'un
genre de caoutchouc aux silicones. Bien que cette plaquette possède la résistance
thermique la moins favorable, elle se distingue par quelques caractéristiques
attrayantes. Selon les informations fournies par le fabricant il n'est plus nécessaire
(puisque parfaitement inutile) de faire appel à la pâte thermoconductrice; la
résistance thermique ne changera pas même en cas d'utilisation de pâte
thermoconductrice. La flexibilité du matériau constitue un second atout de ce genre de
plaquette d'isolation. Elle garantit un bon contact, même sur une surface qui n'est pas
parfaitement plane. Le dernier avantage du silicone est qu'il est virtuellement
impossible, à moins de le faire exprès, de casser une telle plaquette, alors qu'il faut
reconnaître qu'il est relativement aisé de casser une plaquette de céramique ou de
mica.
Dans le coin inférieur droit de la
photo nous voyons finalement quatre rondelles d'isolation servant à isoler les vis
(métalliques) de fixation du boîtier du composant.

Figure 16:
Matériaux pratiques utilisés pour le montage " isolé "
d'un semi-conducteur sur un radiateur. On voit également un petit tube
avec de la pâte thermoconductrice. Cette pâte est appliquée, primo,
entre le semi-conducteur et la plaquette d'isolation et, secundo, entre la plaquette
d'isolation et le radiateur.
La photo de la figure 17 montre une
dizaine de radiateurs courants avec mention de leur résistance thermique. La valeur
réelle de la résistance thermique des radiateurs du type SK71, SK64, SK01 et SK59
dépend de leur longueur, vu qu'il en existe des modèles de différentes longueurs. Les
autres types n'existent qu'en une seule version et leur résistance thermique est donc
fixe. Si l'on compare les résistances thermiques des deux exemplaires du radiateur SK01,
on voit nettement la différence de 10 à 15% qui existe entre la version noire et la
version " non peinte". Notons, une fois encore que les valeurs données des
résistances thermiques ne sont valables que dans le cas d'une disposition verticale des
ailettes de refroidissement du radiateur.
Pour mettre un point final à cet
" historique " des radiateurs nous vous proposons, dans les prochains
paragraphes, quelques instructions de montage.

Figure 17:
Dizaine d'exemplaires de radiateurs courants avec leur résistance thermique.
Le montage :
La première étape du montage d'un
semi-conducteur sur un radiateur consiste à forer des orifices de fixation et (le cas
échéant) des trous par lesquels passeront les broches du composant. Si l'on fait appel
à un radiateur du type "prêt à utiliser" il n'est même pas requis de percer
des trous (ils le sont déjà). La plaquette d'isolation peut rendre d'excellents services
comme gabarit de perçage.
Après avoir indiqué où il faudra
percer les orifices on frappera, à l'aide d'un pointeau et d'un marteau, un petit creux
de centrage dans le radiateur. Ensuite on percera les orifices, chacun avec le diamètre
requis. Les perfectionnistes d'entre nos lecteurs foreront des trous avec un diamètre
plus faible (et d'une profondeur telle que le radiateur ne soit pas percé) pour les doter
ensuite d'un filetage. Cette technique de fixation est plus esthétique et ne demande pas
d'écrous de fixation.
Les croquis des figures 18 et 19 illustrent nettement comment
il faudra monter les deux types principaux de semi-conducteurs sur leur radiateur. Les
composants avec un boîtier TO-3 seront montés, en règle générale, contre la face
extérieure du radiateur, entre les ailettes de refroidissement. Puisque la partie
métallique d'un composant en boîtier TO-3 constitue sa troisième connexion il faudra la
doter d'une languette de soudage permettant de la relier au reste du circuit.

Figure 18:
Technique de montage d'un semi-conducteur
en boîtier TO-3 sur un radiateur. On notera la présence
de la petite languette de soudage, destinée à permettre
la connexion du collecteur du transistor (son boîtier métallique)
au reste de l'électronique.

Figure 19:
Technique de montage pour un semi-conducteur en boîtier TO-220.
Ici on n'aura pas besoin d'une languette de soudage puisque le composant est
doté de ses trois broches de connexion requises.
Pour améliorer la sécurité de
contact ou bien pour éliminer le risque d'un court-circuit accidentel, on pourra doter le
radiateur pour boîtier TO-3 d'une plaquette en aluminium ou en plexiglas, que l'on fait
glisser dans deux entailles prévues à cet effet (figure 20). II existe d'ailleurs des capuchons d'isolation spéciaux pour boîtiers
TO-3.
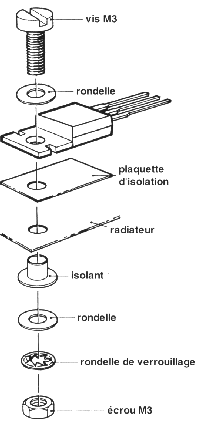
Figure 20:
Pour améliorer (voire garantir) la sécurité
de contact on pourra doter un radiateur du type SK88
d'une petite plaquette en aluminium ou en plexiglas
que l'on glissera dans les entailles prévues à cet effet.
Épilogue :
La transformation en chaleur d'une
puissance P est, dans le cas de régulateurs de tension aussi, égale au produit du
courant de sortie par la différence de tension entre l'entrée et la sortie. S'il s'agit,
par exemple, de refroidir une résistance de puissance (qui, il est vrai, n'est pas un
semi-conducteur) P correspond au produit de la tension à ses bornes par le courant
circulant à travers cette résistance.
La "théorie thermique "
prouve qu'il n'est pas sorcier du tout de dimensionner correctement un radiateur à
utiliser avec l'une ou l'autre application. Une fois que l'on s'est familiarisé avec la
" loi d'Ohm thermique " les calculs sont aussi simples que ceux à effectuer
pour déterminer la valeur totale d'une mise en série de plusieurs résistances.
Article tiré de la revue
Elektor n°191 - Mai 1994
Auteur : inconnu !
|