|
 Schéma
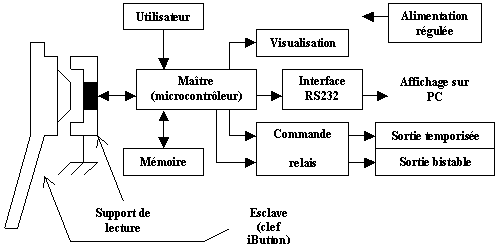
fonctionnel de deuxième degré de la serrure électronique : Schéma
fonctionnel de deuxième degré de la serrure électronique :
 Protocole
d'échange de données avec
le iButton : Protocole
d'échange de données avec
le iButton :
 Etablissement
des rôles entre le microcontrôleur
et le iButton :
Etablissement
des rôles entre le microcontrôleur
et le iButton :
La
lecture des informations contenues dans
la clé est effectuée
par contact momentané du iButton
avec le dispositif de lecture. La transmission
des données
dans un sens ou dans l'autre se fait bit
par bit en commençant par le
bit de poids faible (LSB),
jusqu'à que le message de
64 bits soit
complètement envoyé.
Remplissant
la fonction de maître,
le microcontrôleur
est chargé d'orchestrer le dialogue
avec le iButton,
ce dernier faisant office
d'esclave.
Le maître assure une synchronisation
des bits par l'application d'une transition
de flancs haut / bas sur la ligne de données
selon un protocole très précis.
En fonction du sens de transfert des données,
ce sera soit au maître, soit à
l'esclave d'échantillonner la ligne
1 wire pour en récolter les informations
nécessaires, comme nous allons le
voir ci-après...
 Remise
à zéro (RESET) du iButton :
Remise
à zéro (RESET) du iButton :
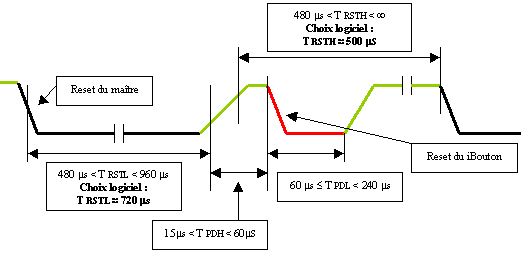
Lorsque
l'on connecte le iButton, le montage alimente
celui-ci. Le maître abaisse le niveau
logique de la ligne 1 wire durant 720µs
toutes les 1 ms en moyenne afin d'initialiser
un éventuel iButton présent
sur la ligne (Master Reset
Pulse) . Pour informer au maître sa présence, le iButton force
la ligne 1 wire à un niveau logique
bas entre 60µs et 240µs,
une
soixantaine de microsecondes après
le niveau logique bas du maître.
 Signal officiel
du RESET (document Dallas) :
Signal officiel
du RESET (document Dallas) :

 Signal
simplifié du RESET :
Signal
simplifié du RESET :
 Oscillogramme
réel du RESET :
Oscillogramme
réel du RESET :

|
En
jaune : la durée du Master
Reset Pulse de 720us
|
|
En
vert : initialisation interne
du composant iButton de l'ordre
de 120us
|
Une
fois cette phase terminée, le niveau
logique bas
forcé
par le iButton est relâché
au profit de la résistance de
pull-up R11
comme ci-dessous :

 Transmission
au iButton du code d'autorisation de lecture
:
Transmission
au iButton du code d'autorisation de lecture
:
Après
le démarrage du processus par un
flanc descendant, la transmission des bits
en direction du composant iButton dans le
cadre de créneaux
d'écriture
(durée comprise entre 60
et 120us)
peut avoir lieu. Cette écriture doit
correspondre au
code d'autorisation de lecture
(code ROM) permettant par la suite le rapatriement
vers le maître des 64 bits du composant iButton.
Ce
code d'autorisation de lecture vaut : $33
= %00110011.
Pour
effectuer cette écriture, le maître
transmet
par une suite de niveaux haut et bas judicieusement
calibrés, le
code d'autorisation de lecture
$33 en commençant par son LSB.
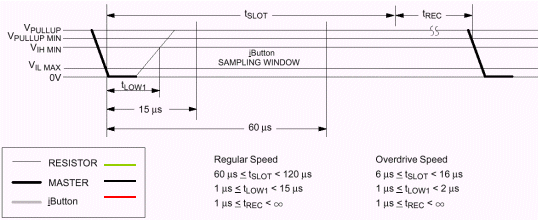
A cet instant, le iButton
échantillonne
la ligne de données de 15µs
à 60µs
après le début du flanc descendant de
la synchronisation. S'il détecte
dans la fenêtre d'échantillonnage
un niveau
haut,
le iButton l'interprète comme un
"1", s'il
découvre un niveau
bas,
il le considère comme un "0".
Il convient en raison de
cette tolérance entre 15µs et 60µs
de veiller à ce que la ligne reste
parfaitement
stable
pendant le dit intervalle.
 Signal
officiel d'écriture d'un "1"
du maître (document Dallas) :
Signal
officiel d'écriture d'un "1"
du maître (document Dallas) :
 Signal
simplifié d'écriture d'un
"1" du maître :
Signal
simplifié d'écriture d'un
"1" du maître :
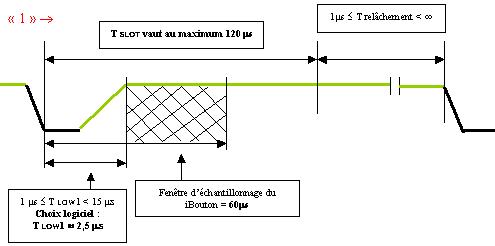
Pour
effectuer l'écriture d'un "1",
le niveau logique de la ligne "1 wire" doit
retourner au niveau
haut 15µs
au
maximum
après le front descendant engendré
par le maître.
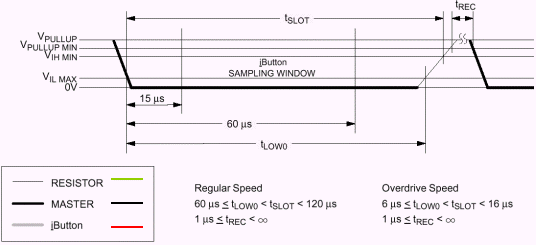
 Signal
officiel d'écriture d'un "0"
du maître (document Dallas) :
Signal
officiel d'écriture d'un "0"
du maître (document Dallas) :
 Signal
simplifié d'écriture d'un
"0" du maître :
Signal
simplifié d'écriture d'un
"0" du maître :

Pour
effectuer l'écriture d'un "0",
le niveau logique de la ligne "1 wire" doit
rester au niveau
bas durant 60µs
au
minimum après
le front descendant engendré par
le maître.
 Oscillogramme
réel d'écriture du code d'autorisation
de lecture $33
= %00110011:
Oscillogramme
réel d'écriture du code d'autorisation
de lecture $33
= %00110011:

 Lecture
des 64 bits d'identification du iButton
:
Lecture
des 64 bits d'identification du iButton
:
Le
composant "1 wire" requiert après écriture
du code $33, un
temps de récupération d'au
minimum 1µs
avant que la transmission ne puisse se poursuivre.
Pour des raisons purement logicielle, le temps
de récupération
choisi dans la présente réalisation
est de l'ordre de 200µs.
Cette surévaluation du temps de récupération
ne pose aucun problème car l'esclave
(le iButton) doit
toujours se plier dans une certaine limite, aux exigences
logicielles du maître (le microcontrôleur).
Le
maître opère de façon
similaire pour la phase de lecture des 64
bits en provenance du composant iButton.
Le maître lance une synchronisation
(front descendant) et doit maintenir cet
état entre 1µs
et 15µs maximum !!!
Le iButton "émet" ensuite le
bit (0 ou 1) de la zone adressée
dans l'espace de la fenêtre d'échantillonnage
du maître.
Deux
cas se profilent :
 Si il s'agit d'un bit "1"
le composant iButton n'a
rien à faire
vu que la ligne de données se trouve
forcée au niveau haut pas une résistance
de pull-up.
Si il s'agit d'un bit "1"
le composant iButton n'a
rien à faire
vu que la ligne de données se trouve
forcée au niveau haut pas une résistance
de pull-up.
 Si il s'agit d'un bit "0"
le composant iButton force
la ligne de données au niveau bas
pendant 15µs au maximum.
Le maître doit avoir échantillonné
la ligne
au cours de cet intervalle,
sinon le bit sera définitivement
perdu... Le iButton met
entre 0 et 45µs pour libérer la ligne
de données.
Si il s'agit d'un bit "0"
le composant iButton force
la ligne de données au niveau bas
pendant 15µs au maximum.
Le maître doit avoir échantillonné
la ligne
au cours de cet intervalle,
sinon le bit sera définitivement
perdu... Le iButton met
entre 0 et 45µs pour libérer la ligne
de données.
La
transmission de la totalité des bits s'effectue à la queue leu
leu en commençant comme toujours
par le LSB pour finir par le MSB des 64 bits
d'identification.
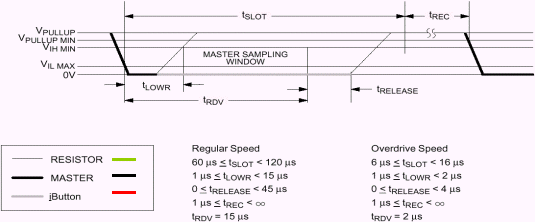
 Signal
officiel de lecture d'un "1" ou
"0" synchronisé par le
maître (document Dallas) :
Signal
officiel de lecture d'un "1" ou
"0" synchronisé par le
maître (document Dallas) :
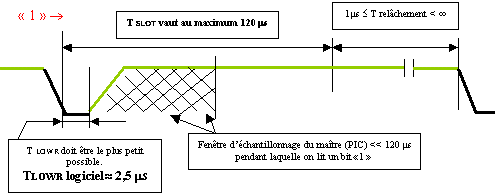
 Signal
simplifié de lecture d'un "1"
synchronisé par le maître : Signal
simplifié de lecture d'un "1"
synchronisé par le maître :
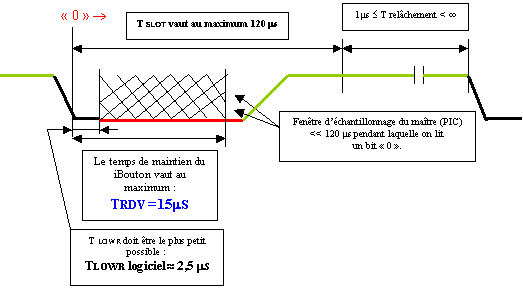
 Signal
simplifié de lecture d'un "0"
synchronisé par le maître : Signal
simplifié de lecture d'un "0"
synchronisé par le maître :
 Oscillogramme
réel des 27 premiers bits
"0" et "1" de ma clé
:
Oscillogramme
réel des 27 premiers bits
"0" et "1" de ma clé
:

Dans
l'oscillogramme précédent,
nous pouvons vérifier
les trois
premiers octets de
la trame 64 bits de ma
clé iButton,
à savoir :
|
Octets
iButton
|
Octet
2
|
Octet
1
|
Code
Family (CF)
|
|
Binaire
|
%00111000
|
%11110000
|
%00000001
|
|
Hexadécimal
|
$38
|
$F0
|
$01
|
|
Décimal
|
56
|
240
|
1
|
Je
vous rappelle que ma
clé iButton
possède le code hexadécimal
64 bits suivant :
$79
$00 $00 $04 $0C
$38
$F0 $01
 Etablissement
du CRC permettant le contrôle d'intégrité
des 64 bits : Etablissement
du CRC permettant le contrôle d'intégrité
des 64 bits :
Toute
la transmission de données fait l'objet
d'un
contrôle d'intégrité
par CRC
(Cyclic Redondance Check) envoyé en fin
de trame (MSB).
Pour
ce faire, le
constructeur Dallas a développé
un procédé permettant de recalculer le CRC
en utilisant un algorithme basé sur
un polynôme 8
bits tel que :
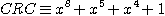
Ainsi,
si la
valeur calculée du CRC
à partir du polynôme 8 bits
est
identique
à la valeur du CRC
lue dans la clé,
on considère la
trame transmise correcte.
Inversement, si il y a inégalité
entre les deux CRC, on considère
la
trame transmise erronée.
Dans
le chapitre qui va suivre, nous allons nous
intéresser à
l'aspect pratique
du code CRC
sans nous soucier de la démonstration
fastidieuse de la précédente
relation. Si vous souhaitez en savoir plus,
consulter les
[ Datasheets
]
fournies avec cette réalisation.
 Table
résultante du polynôme 8 bits
:
Table
résultante du polynôme 8 bits
:
Dallas
démontre que la résultante
du polynôme 8 bits
peut s'écrire sous la forme de 256
valeurs
rassemblées dans une table comme ci-dessous
:
|
N
|
Valeurs
du polynôme = code courant
CRC
|
|
0
|
0
|
94
|
188
|
226
|
97
|
63
|
221
|
131
|
194
|
156
|
126
|
32
|
163
|
253
|
31
|
65
|
|
16
|
157
|
195
|
33
|
127
|
252
|
162
|
64
|
30
|
95
|
1
|
227
|
189
|
62
|
96
|
130
|
220
|
|
32
|
35
|
125
|
159
|
193
|
66
|
28
|
254
|
160
|
225
|
191
|
93
|
3
|
128
|
222
|
60
|
98
|
|
48
|
190
|
224
|
2
|
92
|
223
|
129
|
99
|
61
|
124
|
34
|
192
|
158
|
29
|
67
|
161
|
255
|
|
64
|
70
|
24
|
250
|
164
|
39
|
121
|
155
|
197
|
132
|
218
|
56
|
102
|
229
|
187
|
89
|
7
|
|
80
|
219
|
133
|
103
|
57
|
186
|
228
|
6
|
88
|
25
|
71
|
165
|
251
|
120
|
38
|
196
|
154
|
|
96
|
101
|
59
|
217
|
135
|
4
|
90
|
184
|
230
|
167
|
249
|
27
|
69
|
198
|
152
|
122
|
36
|
|
114
|
248
|
166
|
68
|
26
|
153
|
199
|
37
|
123
|
58
|
100
|
134
|
216
|
91
|
5
|
231
|
185
|
|
128
|
140
|
210
|
48
|
110
|
237
|
179
|
81
|
15
|
78
|
16
|
242
|
172
|
47
|
113
|
147
|
205
|
|
144
|
17
|
79
|
173
|
243
|
112
|
46
|
204
|
146
|
211
|
141
|
111
|
49
|
178
|
236
|
14
|
80
|
|
160
|
175
|
241
|
19
|
77
|
206
|
144
|
114
|
44
|
109
|
51
|
209
|
143
|
12
|
82
|
176
|
238
|
|
176
|
50
|
108
|
142
|
208
|
83
|
13
|
239
|
177
|
240
|
174
|
76
|
18
|
145
|
207
|
45
|
115
|
|
192
|
202
|
148
|
118
|
40
|
171
|
245
|
23
|
73
|
8
|
86
|
180
|
234
|
105
|
55
|
213
|
139
|
|
208
|
87
|
9
|
235
|
181
|
54
|
104
|
138
|
212
|
149
|
203
|
41
|
119
|
244
|
170
|
72
|
22
|
|
224
|
233
|
183
|
85
|
11
|
136
|
214
|
52
|
106
|
43
|
117
|
151
|
201
|
74
|
20
|
246
|
168
|
|
240
|
116
|
42
|
200
|
150
|
21
|
75
|
169
|
247
|
182
|
232
|
10
|
84
|
215
|
137
|
107
|
53
|
Avec
N
représentant l'index
du code courant caractérisé
par la première case de la ligne
considérée.
Exemple : Index 0 = 0, Index 97 = 59, Index
210 = 235, etc...
A
partir de cette table, nous allons calculer
l'octet CRC
en utilisant seulement les
7 octets lus dans la clé,
c'est à dire pour le cas présent
:
$00 $00 $04 $0C
$38
$F0 $01 => 7 octets
et
en appliquant la relation tel que :
CRC
= Table [ Index
du code courant CRC XOR
octet
lu dans la clé ]
Note
: XOR = fonction OU exclusif.
 Exemple
de calcul du code CRC à partir des
7 octets de ma clé Dallas :
Exemple
de calcul du code CRC à partir des
7 octets de ma clé Dallas :
Octets lus dans ma clé iButton :
$00 $00 $04 $0C
$38
$F0 $01 => 7 octets
et
sa valeur CRC lue : $79
mais
qui reste à contrôler !!!
|
Valeurs
courantes du CRC
|
Octets
lus dans la clé
|
Valeurs
de l'index du code courant
|
Valeurs
contenues dans la table
|
|
On
commence toujours par $00
|
CF
= $01
|
$00
XOR $01=$01
1 en décimal
|
Table
[1] = 94
$5E en hexa
|
|
$5E
|
$F0
|
$5E
XOR $F0 = $AE
174 en décimal
|
Table
[174] = 176
$B0 en hexa
|
|
$B0
|
$38
|
$B0
XOR $38 = $88
136 en décimal
|
Table
[136] = 78
$4E en hexa
|
|
$4E
|
$0C
|
$4E
XOR $0C = $42
66 en décimal
|
Table
[66] = 250
$FA en hexa
|
|
$FA
|
$04
|
$FA
XOR $04 = $FE
254 en décimal
|
Table
[254] = 107
$6B en hexa
|
|
$6B
|
$00
|
$6B
XOR $00 = $6B
107 en décimal
|
Table
[107] = 69
$45 en hexa
|
|
$45
|
$00
|
$45
XOR $00 = $45
69 en décimal
|
Table
[69] = 121
$79 en hexa
|
|
$79
|
CRC
= $79
|
$79
XOR $79 =
$00
0
en décimal
|
Table
[0] = 0
$00
en
hexa
|
Vous
pouvez constater que nous avons l'octet
CRC
calculé égal à l'octet
CRC lu dans la clé.
Ainsi nous sommes
certains de
l'exactitude de la trame
lue par le microcontrôleur.
Si
l'octet
CRC calculé était différent
de l'octet CRC lu dans la clé,
nous aurions considéré cette
trame
érronnée.
Simple et efficace !
|